Änderungen an Bauvorschlägen

Immer wieder treten Nachbauer mit der Frage an mich heran, ob und inwieweit bestehende Bauvorschläge abgeändert werden können. Dabei sind die Fragen vollkommen unterschiedlicher Natur und beziehen sich auf unterschiedliche Punkte eines Lautsprechers. Manche solcher Fragen sind recht einfach und eindeutig zu beantworten.  Auf andere wiederum kann man nur schwer bis gar nicht seriös antworten. Aus diesem Grund habe ich diesen kleinen Artikel verfasst, der Antwort auf viele mögliche Fragen geben soll.

Eine der am häufigsten gestellten Fragen ist die, ob die bei einigen Bauvorschlägen vorgesehenen Fasen wirklich notwendig sind, oder ob diese zumindest abgeändert werden können. Dazu sei angemerkt, dass jede auch noch so kleine Variation solcher Fasen eine Veränderung im Amplitudenverlauf und im Abstrahlverhalten nach sich zieht. Wie stark diese Veränderungen sind, ist natürlich von Fall zu Fall verschieden. Die hier folgenden Beispiele zeigen auf, wie sich bereits minimale Veränderungen der Schallwandgeometrie auswirken können. Jeder kann und soll für sich entscheiden, als wie gravierend er die mögliche Veränderung bewertet, und ob er bereit ist, diese in Kauf zu nehmen.

Die folgenden Beispiele zeigen das Verhalten einer unbeschalteten 0,75″ Hochtonkalotte in diversen Schallwänden. Zunächst beträgt die Schallwandbreite 24 cm. Die Kalotte ist mittig montiert. Ihr Zentrum befindet sich 7 cm von der Oberkante der Schallwand mit seitlichen Fasen von 1,5 cm Breite.

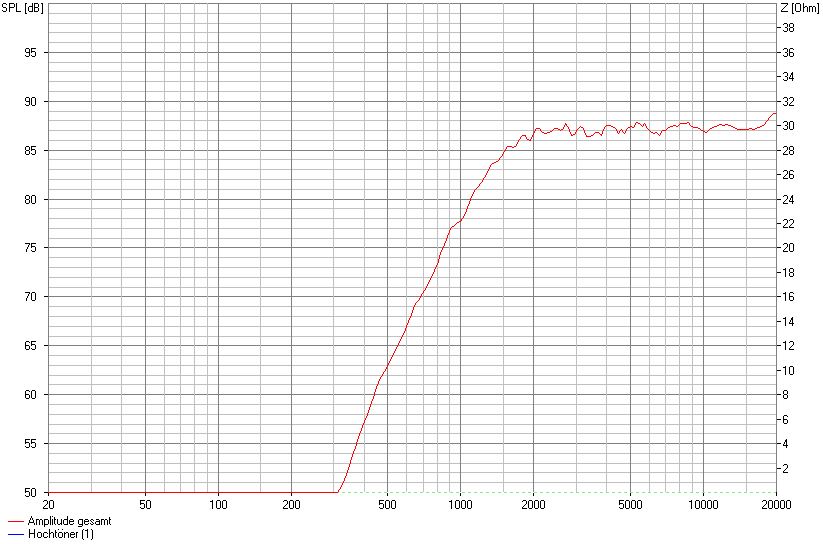SW 24 cm, mittige Montage, 7 cm von OK, 1,5 cm Fasen seitlich

Man sieht einen sehr ausgeglichenen Verlauf der Amplitude mit einer Schwankung von etwa +/- 0,5dB.

Im folgenden Beispiel verbreitern wir die Fasen um 0,5 cm auf 2 cm bei ansonsten vollkommen identischer Position des Hochtöners. Als Referenz ist die ursprüngliche Position gestrichelt hinterlegt.

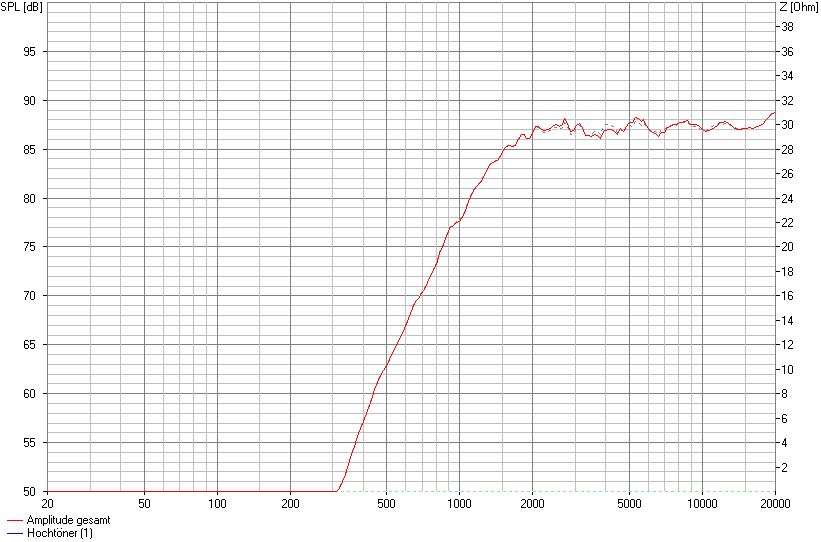SW 24 cm, mittige Montage, 7 cm von OK, 2,0 cm Fasen seitlich

Bereits diese recht kleine Veränderung von nur 0,5 cm je Fase beeinflußt den Verlauf der Amplitude merklich. Wir wollen das Spiel aber weiter spielen und erhöhen die Breite um weitere 0,5 cm auf 2,5 cm.

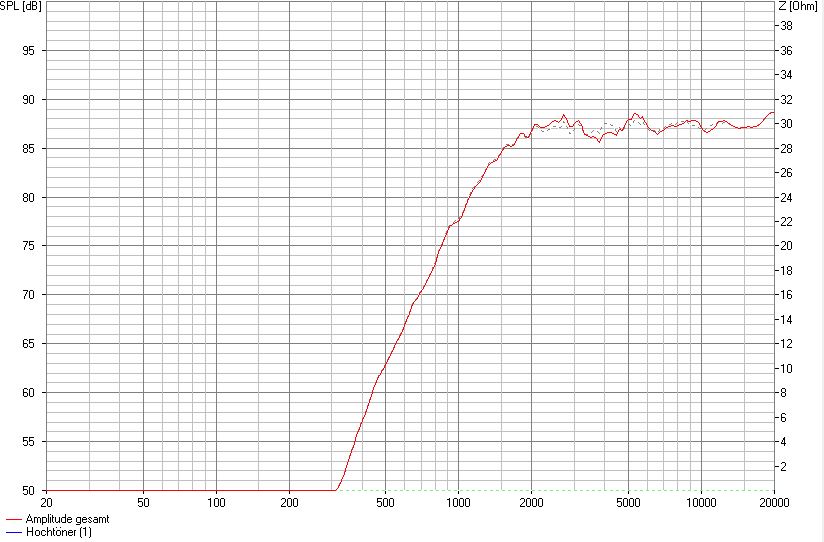
SW 24 cm, mittige Montage, 7 cm von OK, 2,5 cm Fasen seitlich

Ganz offensichtlich nimmt die Linearität durch die Veränderung der Fase weiter ab. Wir erhöhen nochmals um weitere 0,5 cm auf insgesamt 3 cm Breite.

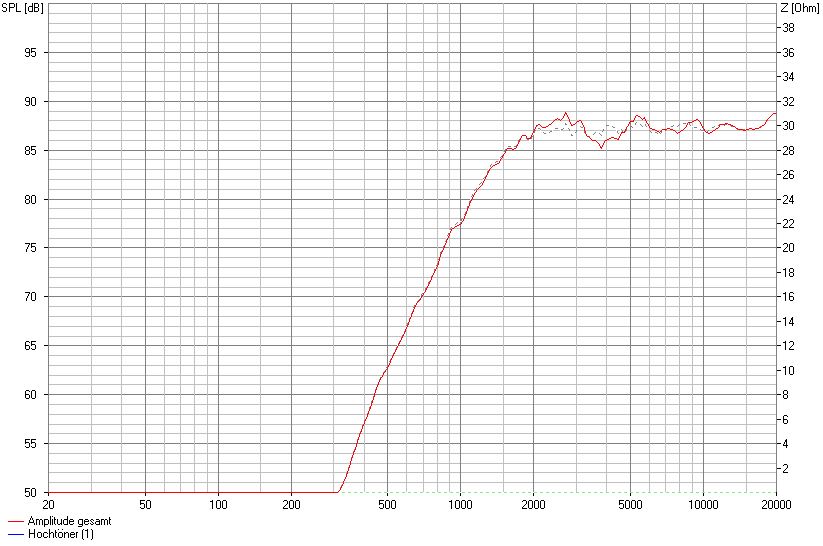
SW 24 cm, mittige Montage, 7 cm von OK, 3,0 cm Fasen seitlich

Der Einbruch bei rund 4 kHz wird durch die Veränderung der Fase noch einmal kräftiger.

Nun könnte man annehmen, dass eine Vergrößerung der Fase automatisch mit einer schlechteren Linearität einhergeht. Das ist natürlich nicht der Fall, und das hängt von vielen weiteren Faktoren ab. Da spielen z. B. auch die Position des Chassis und dessen Ausführung eine nicht zu unterschätzende Rolle. Ist die Frontplatte des Chassis plan, oder ist sie wie ein Waveguide geformt? Ragt die Kalotte über eine plane Frontplatte hinaus, oder liegt sie hinter der Ebene ihrer Frontplatte? Natürlich fließt auch der Durchmesser ein. All diese Dinge nehmen Einfluß auf die Linearität und das Abstrahlverhalten unter Winkeln, welches in den hier gezeigten Beispielen nicht aufgeführt wird.  Was passiert aber, wenn man bei ebenfalls unveränderter Einbauposition beim gezeigten Beispiel komplett auf die Fasen verzichtet?

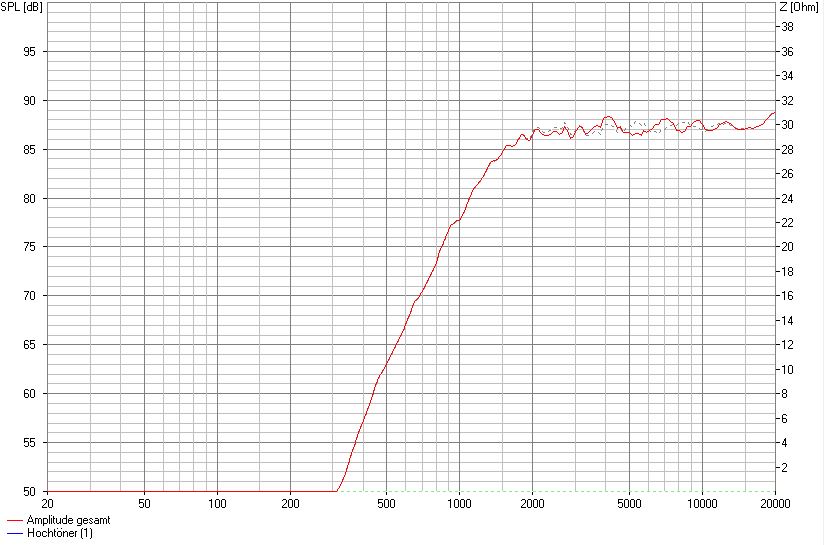
SW 24 cm, mittige Montage, 7 cm von OK, keine Fasen seitlich

Das Beispiel zeigt, dass ein kompletter Verzicht auf Fasen ebenfalls zu einer Verschlechterung der Amplitude führt.

Häufig wird auch die Frage gestellt, was denn passiert, wenn man etwas an der Position eines Chassis auf der Schallwand verändert. Natürlich hat auch das Auswirkungen auf die Linearität. Die folgenden Beispiele zeigen die möglichen Auswirkungen.

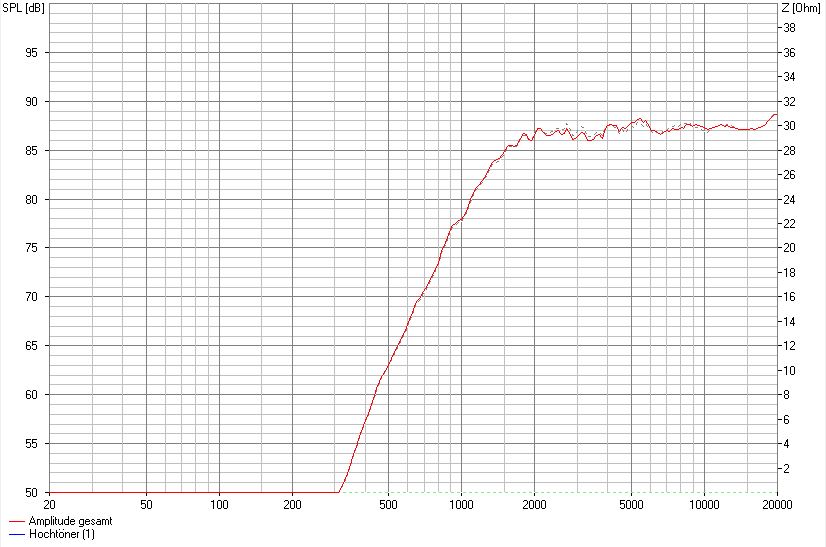
SW 24 cm, mittige Montage, 8 cm von OK, 1,5 cm Fasen seitlich

Die Schallwand entspricht wieder der Ausgangssituation mit 1,5 cm breiten Fasen. Lediglich die Position des Chassis ist um 1 cm nach unten gerutscht. Wieder verändert sich die Linearität zum Schlechteren. Versetzen wir den Töner noch einen cm weiter nach unten

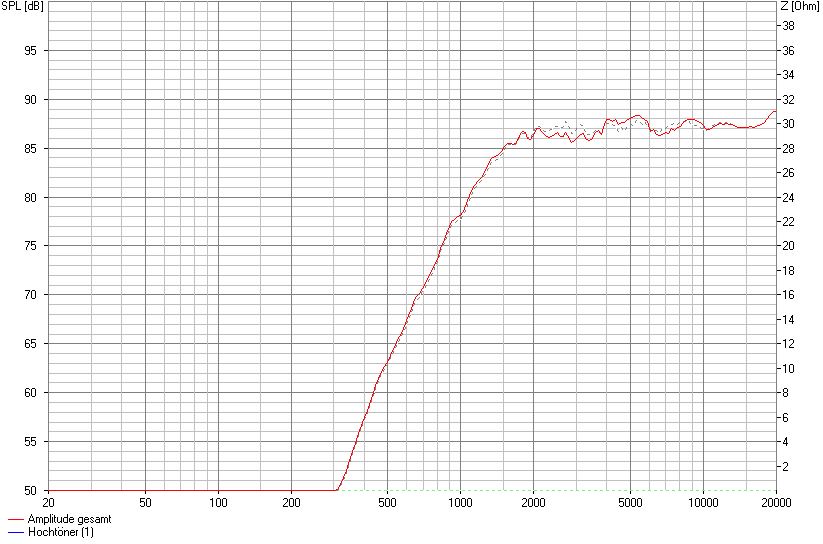
SW 24 cm, mittige Montage, 9 cm von OK, 1,5 cm Fasen seitlich

Eine weitere Verschlechterung ist die Folge. Verändern wir zusätzlich noch die Fasen.

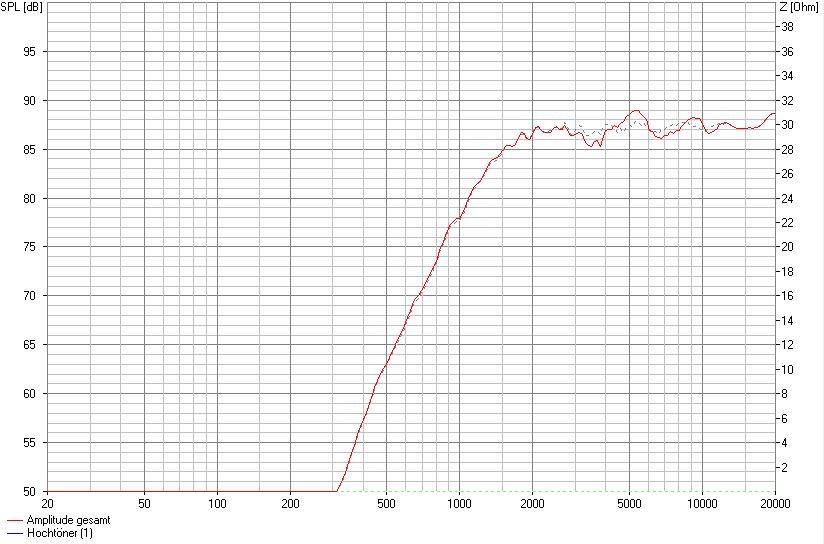
SW 24 cm, mittige Montage, 9 cm von OK, 2,5 cm Fasen seitlich

Der Frequenzgang wird durch die größeren Fasen noch einmal schlechter. Diese Auswirkung wäre definitiv hörbar.

Hier nun das Verhalten komplett ohne Fasen.

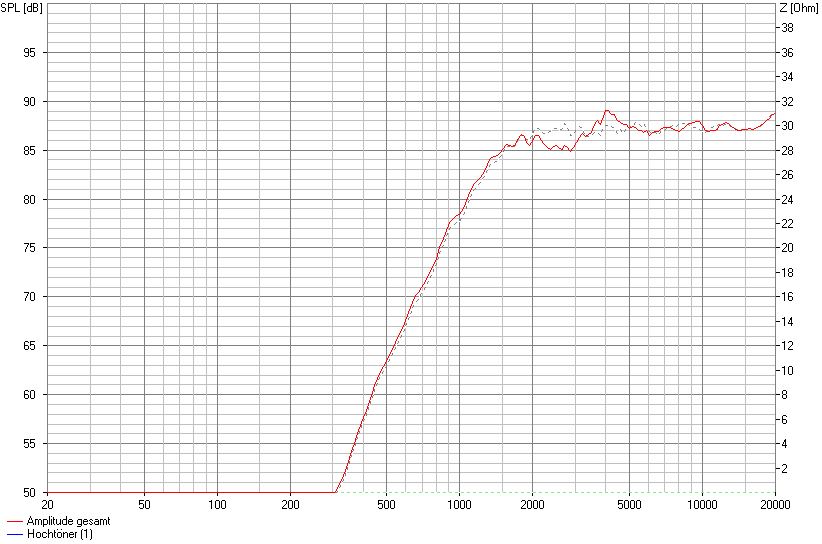
SW 24 cm, mittige Montage, 9 cm von OK, keine Fasen seitlich

Die Linearität wird deutlich schlechter und ist vollkommen inakzeptabel.

Nun verändern wir zusätzlich noch die Breite des Gehäuses.

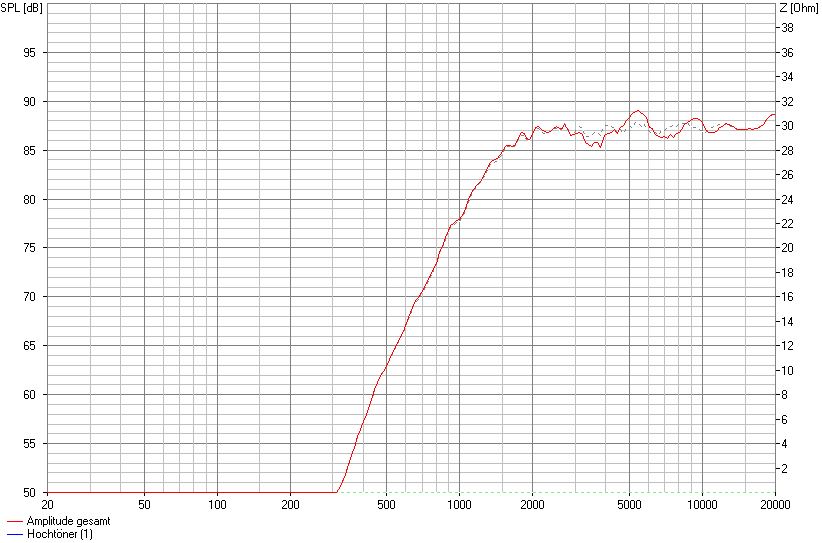
SW 23 cm, mittige Montage, 9 cm von OK, 2,5 cm Fasen seitlich

Eine zusätzliche Fase oberhalb des Chassis sorgt für eine weitere Veränderung.

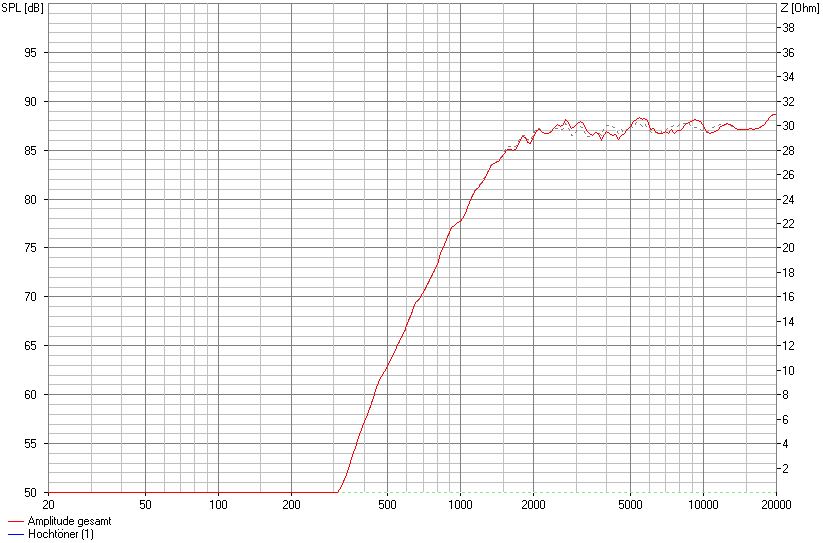
SW 23 cm, mittige Montage, 9 cm von OK, 2,5 cm Fasen seitlich und 2,5 cm Fase oben

Hier wird das Gehäuse um 1 cm verbreitert mit lediglich seitlichen Fasen

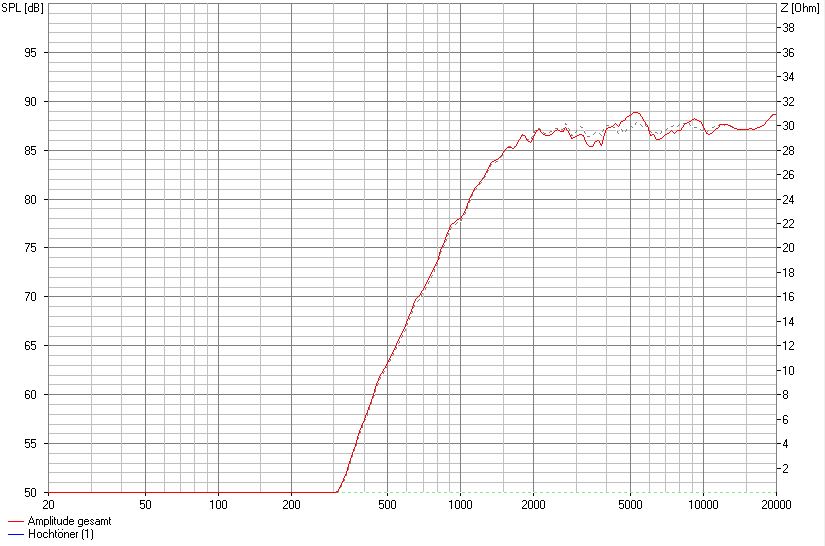
SW 25 cm, mittige Montage, 9 cm von OK, 2,5 cm Fasen seitlich

Und zuletzt eine deutliche Verbreiterung mit 1,5 cm breiten seitlichen Fasen.

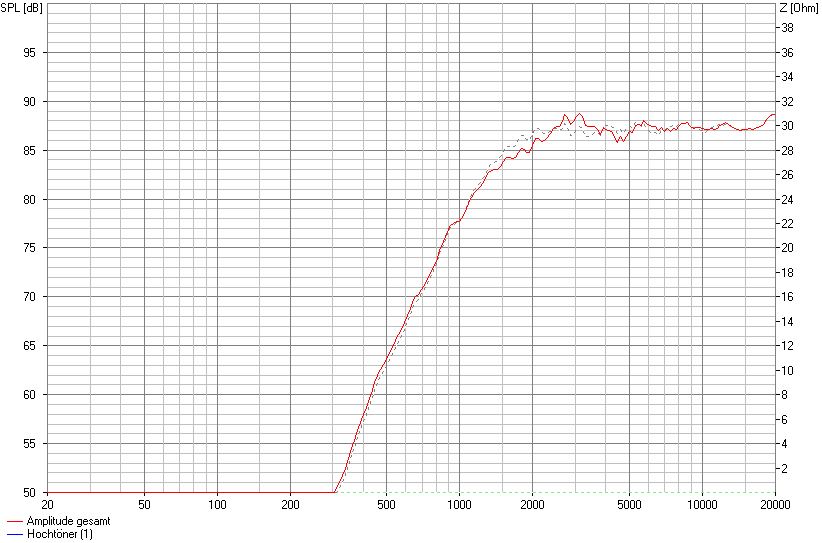
SW 32 cm, mittige Montage, 7 cm von OK, 1,5 cm Fasen seitlich

Wir sehen, dass jede noch so kleine Veränderung an der Schallwandgeometrie und der Position des Chassis auf der Schallwand zu Veränderungen führt. Gerade das letzte Beispiel zeigt, dass es eine hanebüchene Idee ist, einen ursprünglich aus zwei oder mehreren aufeinander stehenden, unterschiedlich großen Einzelgehäusen bestehenden Lautsprecher ggfs. einteilig mit durchgehender Breite aufzubauen.

Im Zusammenhang mit dem geplanten Einsatz von Lautsprechern im Rahmen eines Heimkinos wünschen eventuelle Nachbauer häufig, einen bestehenden Bauvorschlag in der Tiefe zu verringern und dafür die Höhe und die Breite zu vergrößern. So könnte der Lautsprecher als Wandlautsprecher betrieben werden. Natürlich würde bei einem solchen Umbau das Volumen des Lautsprechers identisch bleiben. Eine Vergrößerung der Länge unterhalb der Chassis wäre unter Beibehaltung der Chassisabstände zur Oberkante und zueinander zwar ohne nennenswerte Veränderungen möglich. Die Verbreiterung eines Lautsprechers wäre aber wegen der o. g. Veränderungen nicht zielführend. Es käme aber noch ein weiterer Faktor hinzu, der die korrekte Funktion des Lautsprechers vereiteln würde. I. a. R. sind Standlautsprecher und auch die meisten Kompakten so konzipiert, dass sie mit einigem Abstand zu den Wänden frei aufgestellt werden müssen.

Lautsprecher abgestimmt für freie Aufstellung

Betreibt man einen solchen, für freie Aufstellung konzipierten Lautsprecher direkt an einer Wand, führt dies zu einem deutlichen Pegelanstieg im Bassbereich und einer entsprechend unnatürlichen Wiedergabe.

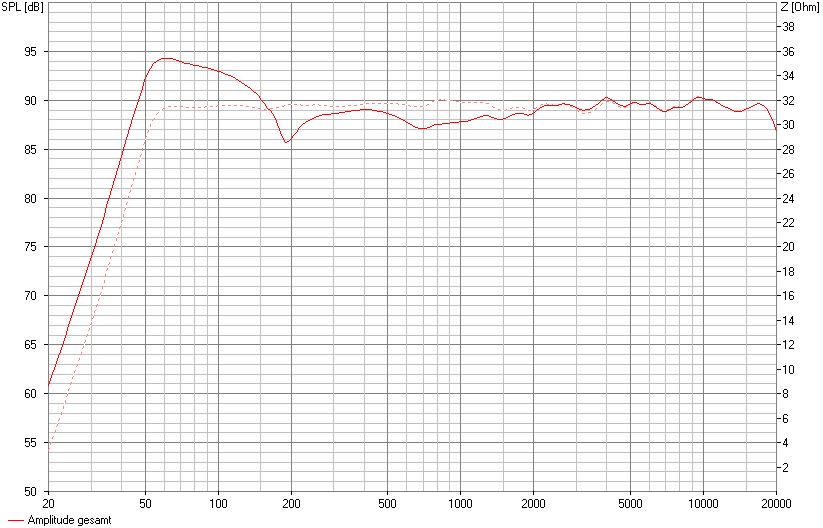
Lautsprecher abgestimmt für freie Aufstellung direkt an der Wand betrieben

Eine weitere beliebte Frage dreht sich um die Bedämpfung eines Lautsprechergehäuses und die mögliche Verwendung eines alternativen, weil günstigeren oder bereits vorhandenen Bedämpfungsmaterials.  Diese Frage lässt sich in der Praxis auch kaum beantworten. Das liegt daran, dass unterschiedliche Materialien unterschiedliche Bedämpfungskoeffizienten aufweisen. Natürlich kann eine seriöse Aussage darüber, ob ein alternatives Material auch funktionieren könnte, nicht ohne Messungen beantwortet werden.  Ein paar mit dem MJK Sheet erstellte Simulationen zeigen den Einfluß bestimmter Bedämpfungskoeffizienten ohne weitere Veränderungen an der eigentlichen Abstimmung in einem 80 cm hohen Gehäuse.

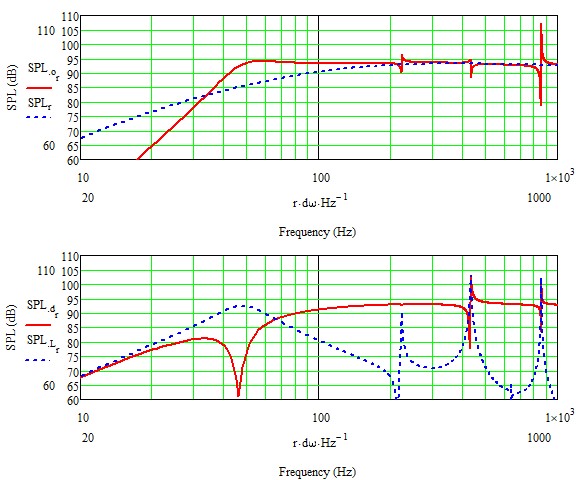Chassis in Gehäuse unbedämpft

Deutlich sieht man die bei einer Gehäusehöhe von 80 cm auftretende stehende Welle bei rund 214 Hz und ihre Vielfachen. (Schallgeschwindigkeit/2/Höhe in Metern = 343/2/0,8 ~ 214)

Mit Erhöhung des Bedämpfungskoeffizienten verringert sich die Ausprägung der stehenden Welle entsprechend.

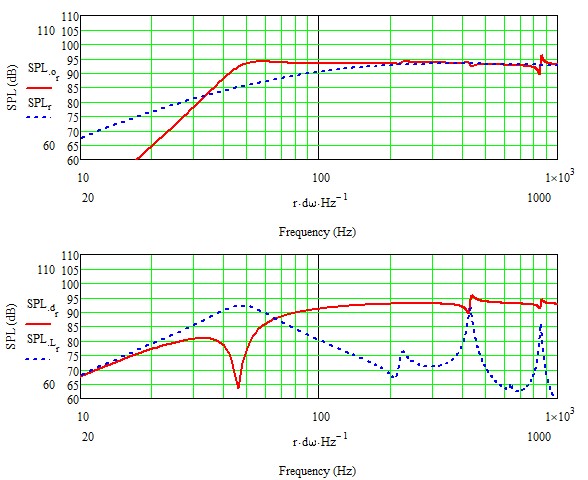
Chassis in Gehäuse schwach bedämpft

Optimal bedämpft wirken sich die entstehenden Resonanzen nicht mehr störend auf den Verlauf der Amplitude aus.

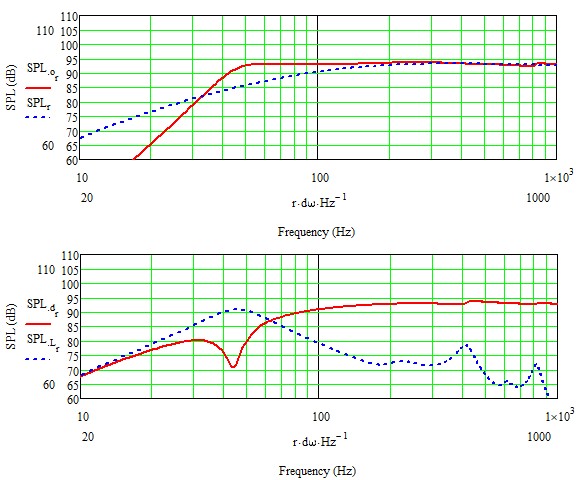
Chassis in Gehäuse optimal bedämpft

Noch särkere Bedämpfung führt zwar einerseits zu einer noch wirksameren Bedämpfung der Resonanzen. Auf der anderen Seite wird aber auch die Intensität der Basswiedergabe bereits beeinträchtigt. Es kommt zu einem Abfall.

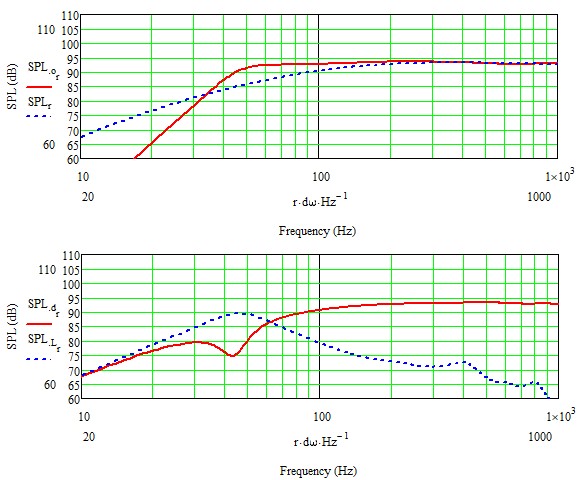
Chassis in Gehäuse stärker bedämpft

Bei weiterer Steigerung der Bedämpfung nähert sich das Verhalten dem eines geschlossenen Lautsprechers an. Der BR Port verliert allmählich seine Wirkung. Dies passiert auch, wenn der „Weg“ zwischen Chassis und Port durch Bedämpfungsmaterial verstopft ist.

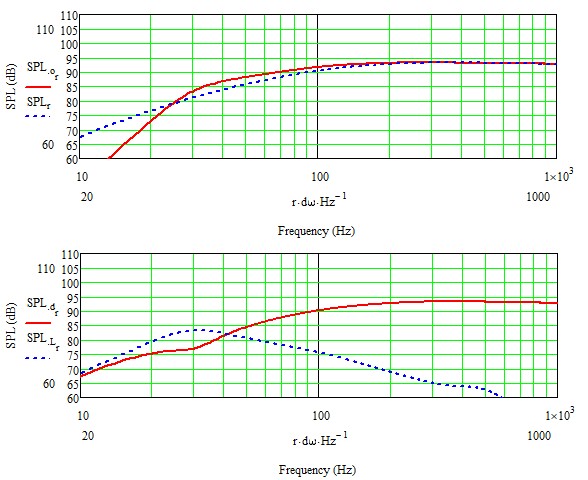
Chassis in Gehäuse überbedämpft

Für all diejenigen, die mit den MJK Darstellungen nicht ganz so vertraut sind, eine kurze Erklärung. Die jeweils obere Grafik in den Doppelabbildungen zeigt den von Membran und Port gemeinsam erzeugten Schall (rot) im Vergleich zu dem, was das Chassis in einer CB mit identischem Volumen erzeugen würde (blau gestrichelt). Die jeweils untere Grafik zeigt den Membranschall (rot) und den jeweiligen Portanteil samt Resonanzen (blau gestrichelt) in der BR Konfigurarion. Also entspricht die rote Kurve der jeweils oberen Grafik der phasenkorrigierten Summe aus roter und blau gestrichelter Kurve der jeweils unteren Grafik.

Eine Frage, die hier ebenfalls beantwortet werden soll, dreht sich um die Auswahl eines Ports. Die Vielzahl der abgebotenen Rohre ist schier unendlich. Es gibt auch gewaltige Preisunterschiede. Deswegen empfehle ich nur ganz selten die Verwendung eines bestimmten Fabrikats, sondern gebe lediglich einen Durchmesser an. In der Praxis ist es egal, ob der effektive Durchmesser eines angenommenen 70 mm Ports nun 69 mm oder 71 mm beträgt. Es ist auch nicht wichtig, ob der auserkorene Port leicht konisch zuläuft oder nicht. Die daraus resultierenden Unterschiede in der Abstimmung sind so gering, dass weitere Toleranzen beim Gehäusevolumen, eventuelle Undichtigkeiten des Gehäuses und nicht zuletzt die Aufstellung des Lautsprechers zu größeren Unterschieden führen.

Letztes Thema im Rahmen dieser kleinen Abhandlung sollen Frequenzweichenbauteile sein. Häufig werden in Weichenschaltbildern Widerstandswerte bei den Spulen angegeben. Je nach Hersteller variieren diese Werte bei gleichen Induktivitäten. In Fällen, in denen Spulen in Reihe zum Chassis liegen, ist es kein Problem, eine Spule zu wählen, deren Widerstand dem angegebenen Wert nah kommt. Kleinere Abweichungen sind problemlos möglich.

Angenommen, es handelt sich um eine 18dB Beschaltung für einen Tieftöner wie folgt

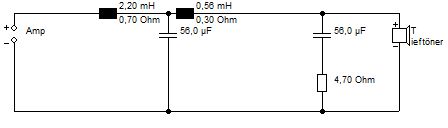Spulenwiderstände 0,7 Ohm und 0,3 Ohm

Im Sortiment von Jantzen Audio finden sich eine 2,2 mH Luftspule  und eine 0,56 mH Luftspule mit 1 mm Draht und 0,8 Ohm bzw. 0,36 Ohm Widerstand.

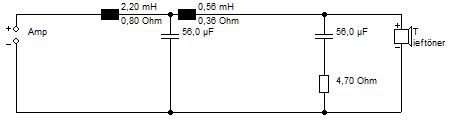Spulenwiderständer 0,8 Ohm und 0,36 Ohm

Der Pegelunterschied würde sich im Bereich von etwa 0,3 dB bewegen, was in der Praxis absolut bedeutungslos ist.

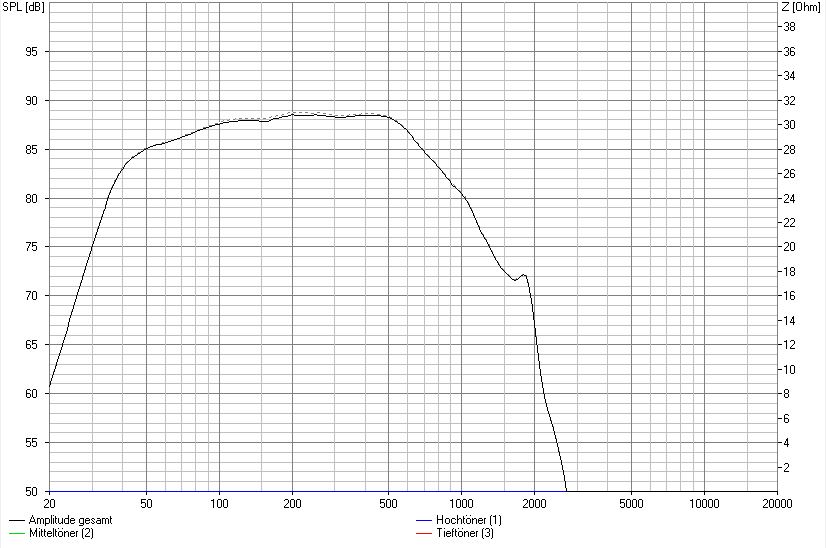
Pegelunterschied durch leicht erhöhten Spulenwiderstand

Bei Verringerung der Spulenwiderstände auf 0,6 Ohm und 0,25 Ohm erhöht sich der Pegel geringfügig, ebenfalls im vernachlässigbaren Bereich.

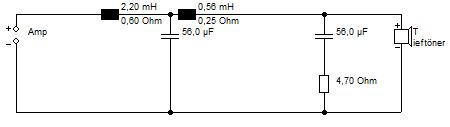Spulenwiderstände 0,6 Ohm und 0,25 Ohm

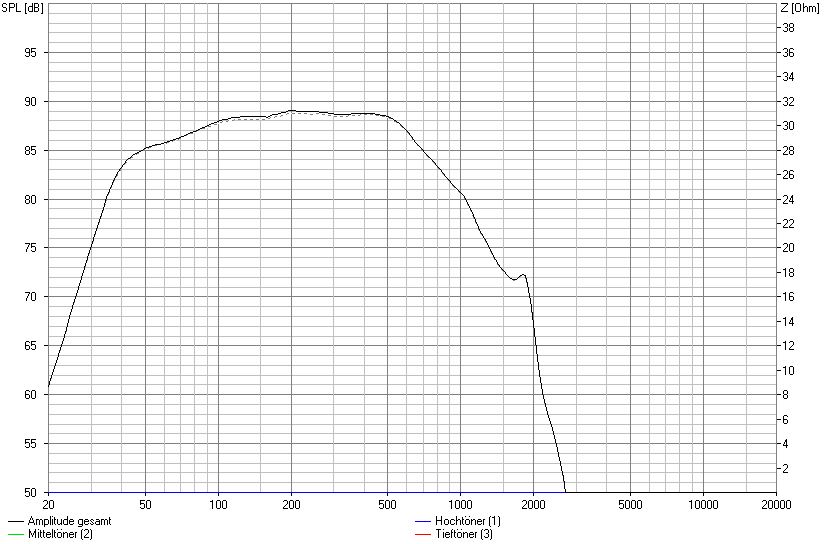
Pegelunterschied durch leicht verringerten Spulenwiderstand

Sobald es sich um Spulen handelt, die Bestandteil eines Saugkreises sind, wird die Intensität der Wirkung dieses Korrekturglieds durch den Gesamtwiderstand des Kreises bestimmt.

Ein mit einer 22 mH Spule aus dem Visaton Sortiment gebildeter Saugkreis weist zusammen mit dem physischen Widerstand insgesamt 10,8 Ohm auf.

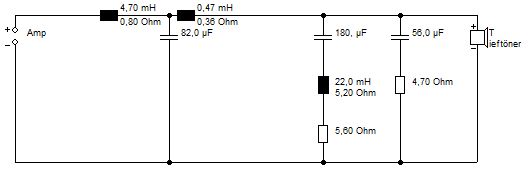Saugkreis mit 10,8 Ohm Gesamtwiderstand

Seine Wirkung zeigt sich wie folgt.

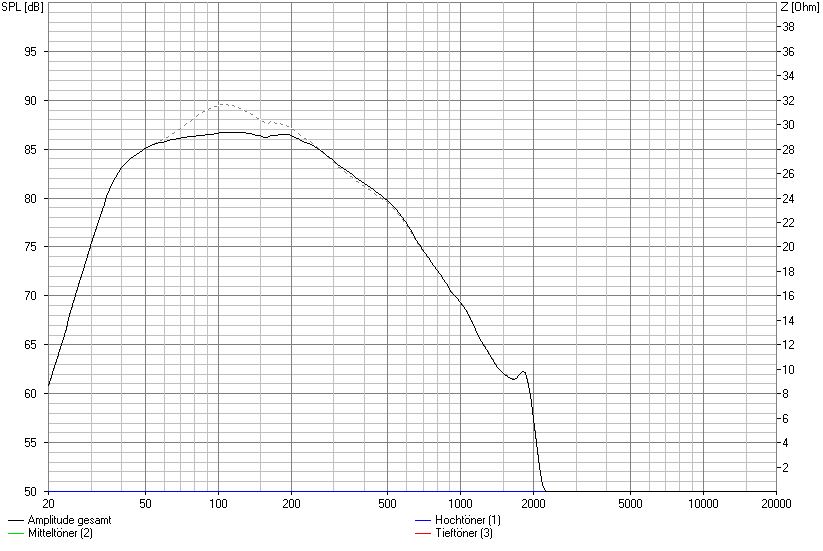Wirkung Saugkreis mit Gesamtwiderstand 10,8 Ohm

Verringert man nun den Gesamtwiderstand um 1 Ohm auf insgesamt 9,8 Ohm,

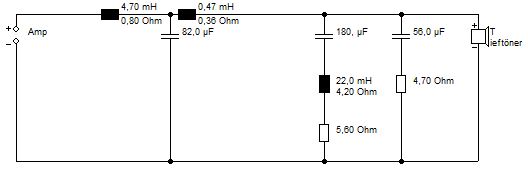
Saugkreis mit 9,8 Ohm Gesamtwiderstand

wirkt sich das wie folgt aus

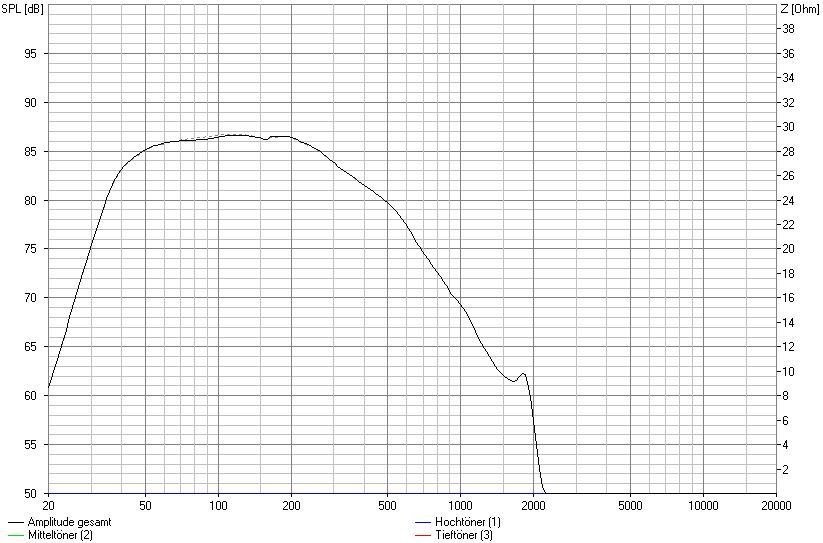Wirkung Saugkreis mit Gesamtwiderstand 9,8 Ohm

Der Unterschied ist kaum sichtbar, geschweige denn hörbar. Gleiches gilt bei entsprechender Erhöhung des Gesamtwiderstands auf beispielhafte 11,8 Ohm

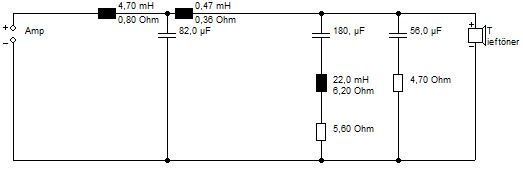
Saugkreis mit 11,8 Ohm Gesamtwiderstand

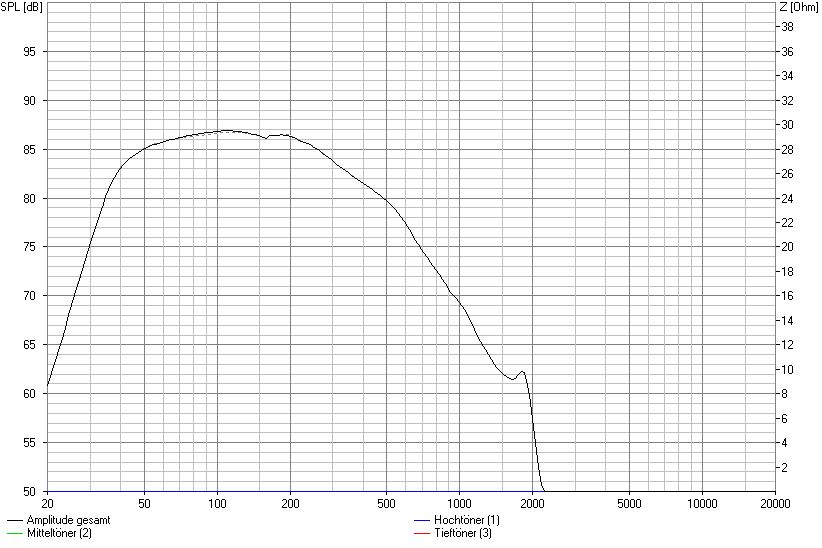
Wirkung Saugkreis mit Gesamtwiderstand 11,8 Ohm

Auch die Vergrößerung des Widerstands ist in der Praxis nicht von Bedeutung. Bei Saugkreisen ist immer der Wert des Gesamtwiderstands zu betrachten. Hier bietet es sich an, die preiswertest mögliche Spule, oder ein vorhandenes Exemplar aus der Bastelkiste  zu verwenden und den notwendigen Gesamtwiderstand über den physischen Widerstand möglichst genau einzustellen.

Ähnlich verhält es sich bei Verwendung eines Sperrkreises. Hier wird der Gesamtwiderstand aus einer Parallelschaltung des Spulenwiderstands und des physischen Widerstands gebildet. Im Jantzen Sortiment findet sich eine 0,22 mH Spule aus 0,7 mm Draht mit einem Widerstand von 0,35 Ohm.

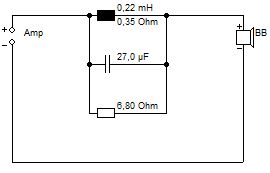Sperrkreis mit Spulenwiderstand 0,35 Ohm

Dieser Sperrkreis korrigiert den Effekt des Baffle Steps bei einem fiktiven Breitbänder wie folgt

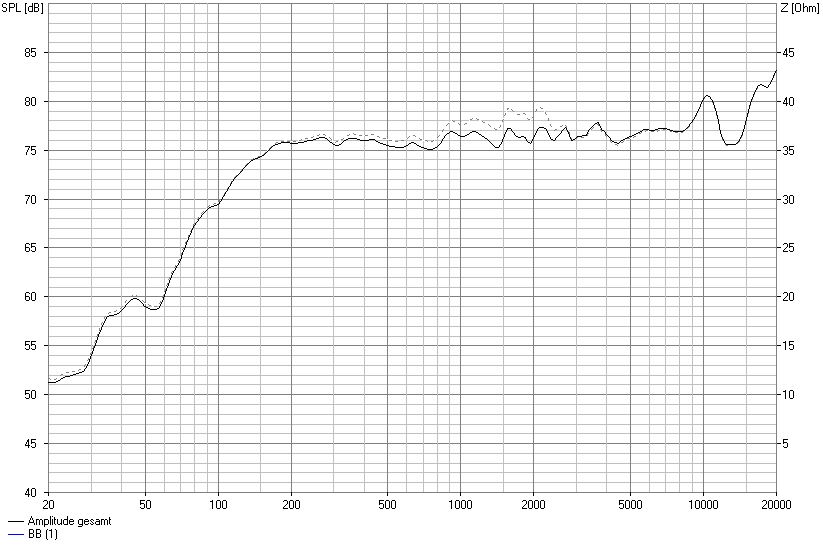
Wirkung Saugkreis mit Spulenwiderstand 0,35 Ohm (Gesamtwiderstand 0,333 Ohm)

Verringern wir nun den Spulenwiderstand auf willkürlich gewählte 0,2 Ohm

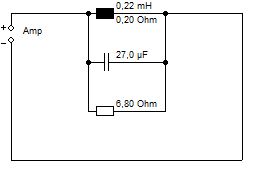
Sperrkreis mit Spulenwiderstand 0,2 Ohm

Der Unterschied ist in der Simulation zwar sichtbar, geht jedoch über Pixelbreite nicht hinaus.

Wirkung Saugkreis mit Spulenwiderstand 0,2 Ohm (Gesamtwiderstand 0,194 Ohm)

Im letzten Experiment wird der Spulenwiderstand um 0,15 Ohm auf 0,5 Ohm angehoben.

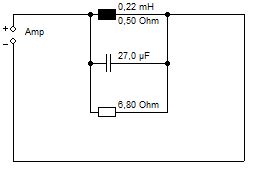
Sperrkreis mit Spulenwiderstand 0,5 Ohm

Auch in diesem Beispiel ist die Abweichung kaum wahrnehmbar.

Wirkung Saugkreis mit Spulenwiderstand 0,5 Ohm (Gesamtwiderstand 0,466 Ohm)

Die kaum sichtbare Abweichung ist natürlich auch bei etwas erhöhtem Spulenwiderstand absolut unbedeutend.

Und nun wünsche ich viel Spaß und Erfolg beim Aufbau des Traumlautsprechers, welcher immer es auch werden wird.