Seien wir doch einfach mal ehrlich. Haben wir nicht alle in den Anfängen unseres Hobbys versucht, die Frequenzweiche unseres Traumlautsprechers mittels eines der vielen online zu findenden Frequenzweichenrechnern zu entwickeln? Ich kann sogar so lange zurückblicken, dass ich mich noch an die manuelle Anwendung des Formelwerks erinnere, auf deren Basis diese Rechner allesamt basieren.
Das Gute an diesen Formeln und Rechnern ist, dass sie einwandfrei funktionieren. Dumm ist, dass sie das leider nicht bei der Entwicklung von Frequenzweichen tun und somit unbrauchbar sind.
Soll das nun bedeuten, dass Frequenzweichenrechner funktionieren, gleichzeitig aber nicht funktionieren? Es mag verrückt klingen, aber leider ist genau das der Fall.
Der folgende Artikel erklärt nicht, welche Wege und Schritte erforderlich sind, um eine funktionierende Frequenzweichenabstimmung durchzuführen. Er soll lediglich am einfach skizzierten Beispiel eines 2-Wege Lautsprechers aufzeigen, dass eine berechnete Weiche in der Praxis nicht funktionieren kann.
Die Frequenzweichenrechner bedienen sich eines Formelwerks aus der Elektrotechnik. Vorgesehen sind diese Formeln für die Berechnung von Filtern mit konstanten Lastwiderständen. Genau diese bringt ein Lautsprecherchassis aber nicht mit. Die bei einem Lautsprecherchassis angegebene Nennimpedanz bezieht sich nach Definition auf die Impedanz, die das Chassis bei 1kHz aufweist. Allerdings wird dieser Wert in der Praxis nur selten eingehalten. Gerade bei Tieftönern liegt die Impedanz bei 1kHz bereits vielfach höher.
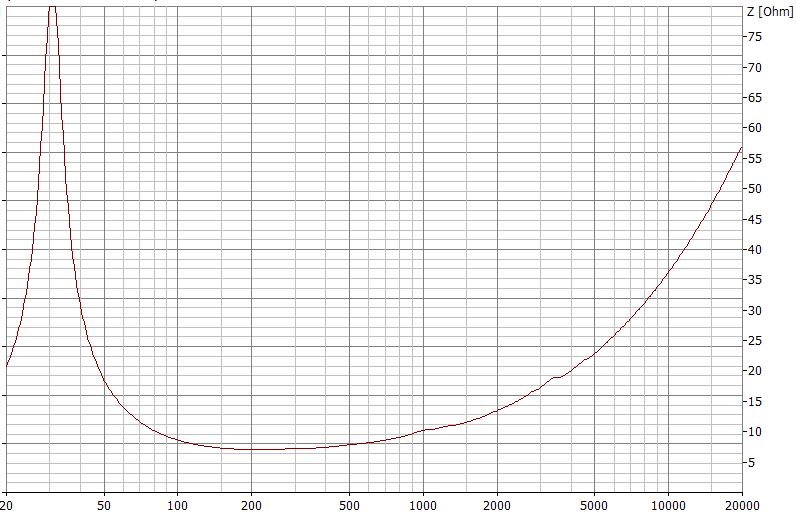
Typischer Impedanzverlauf eines 8 Ohm Tieftöners
Allein die obige Grafik sollte schon erklären, dass eine Frequenzweiche, die mit einem Onlinetool für eine angenommene Trennfrequenz von 2,5 kHz und ein Chassis mit 8 Ohm Nennimpedanz berechnet wurde, nicht wie gewünscht funktionieren wird.
Es gibt aber noch weitere Parameter, die ein Frequenzweichenrechner nicht einbezieht. Denn natürlich hat ein Lautsprecherchassis auch einen Amplitudenverlauf über die Frequenz. Dieser „Frequenzgang“ ist, genau wie der Impedanzverlauf, auch nicht linear. Dumm ist, dass der Frequenzweichenrechner das nicht weiß. Brav wie er ist, geht er nämlich von vollkommener Linearität des Chassis aus.
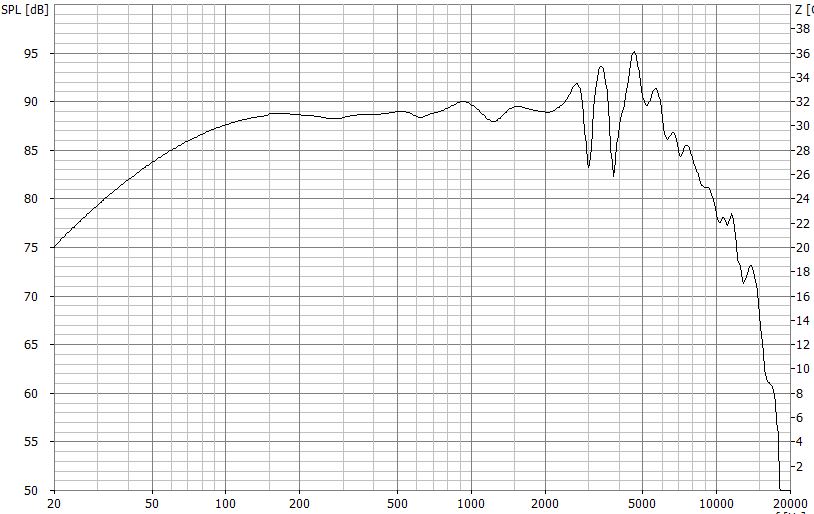Frequenzgang eines unbeschalteten Tieftöners in unendlicher Schallwand
Wie wir sehen, verläuft dieser Tieftöner zwar in seinem vorgesehenen Frequenzbereich recht linear, aber an seinem oberen Ende neigt er zu unschönen und gutem Klang nicht zuträglichen Resonanzen.
Betrachten wir nun einen typischen Kalotten Hochtöner, den wir im weiteren Verlauf dieses virtuellen Projekts zusammen mit dem obigen Tieftöner zu einem 2-Wege Lautsprecher vereinen wollen.
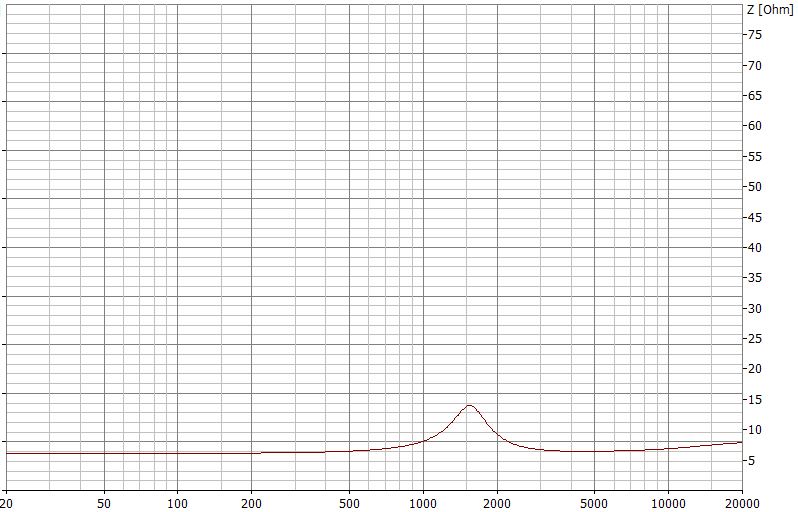Impedanzverlauf eines 8 Ohm Hochtöners
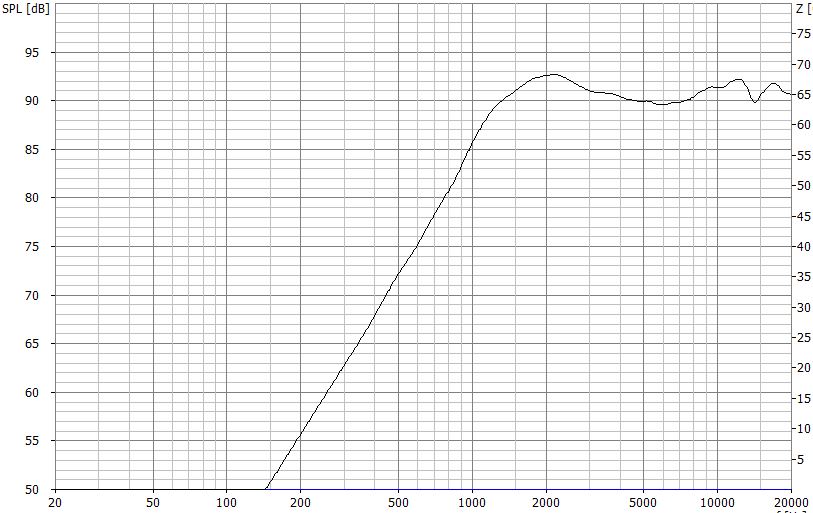
Frequenzgang eines unbeschalteten Hochtöners in unendlicher Schallwand
Es kommt aber noch ein weiterer Parameter hinzu, den ein Weichenrechner nicht berücksichtigen kann. Die oben gezeigten Frequenzgänge von Tieftöner und Hochtöner entsprechen dem Einbau in eine unendliche Schallwand. Diese muss man sich, wie der Name sagt, unendlich groß vorstellen. In der Praxis wollen wir die Chassis aber in ein schmuckes Gehäuse mit Wohnraum tauglichen Maßen einbauen. Und, wir vermuten richtig, dieses verbiegt die Frequenzgänge der Chassis auch noch einmal. Beim Hochtöner ist der Unterschied nicht ganz so dramatisch, aber beim Tief(mittel)töner wirkt sich das drastisch aus.
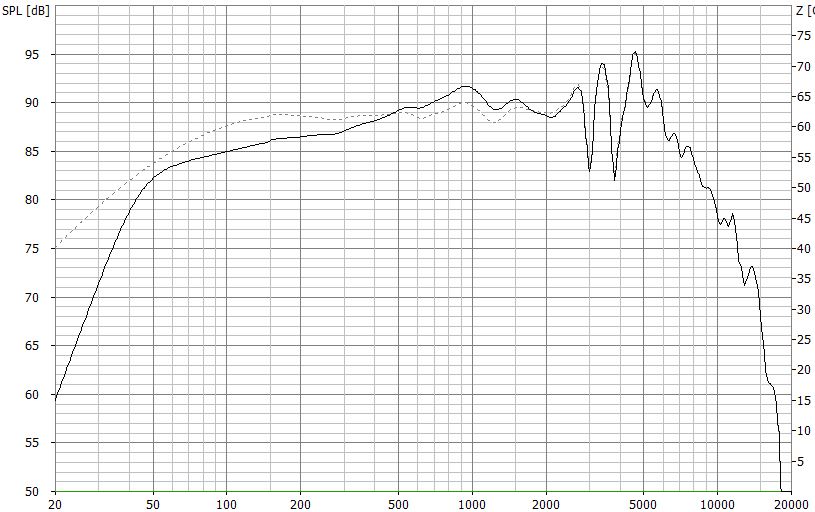Frequenzgang des o. g. Tieftöners in 24cm breiter Schallwand
Wie wir sehen, verliert der Tieftöner unterhalb von 500 Hz deutlich an Schalldruck. Im Mitteltonbereich kommt es hingegen zu einer Überhöhung.
Wagen wir nun einen Blick auf das Verhalten des Hochtöners in der 24cm breiten Schallwand.
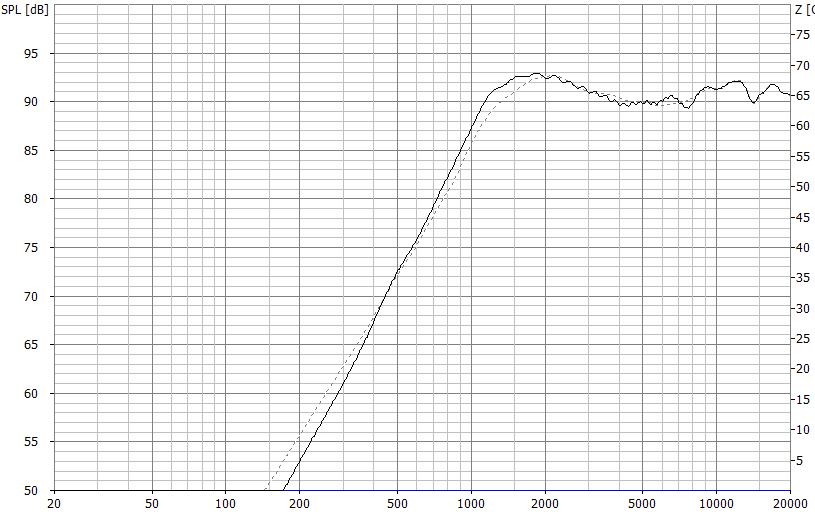Frequenzgang des o. g. Hochtöners in 24cm breiter Schallwand
Auch hier können wir eine Veränderung feststellen, die aber nicht so deutlich ins Gewicht fällt, wie es beim Tief(mittel)töner der Fall ist.
Im nächsten Schritt wagen wir uns an einen der gängigen Frequenzweichenrechner. Der Bequemlichkeit halber wählen wir den Rechner aus der Software Boxsim. Wir tragen 2500 Hz als gewünschte Trennfrequenz ein. Sowohl für den Tieftöner, als auch für den Hochtöner wählen wir 8 Ohm Impedanz.
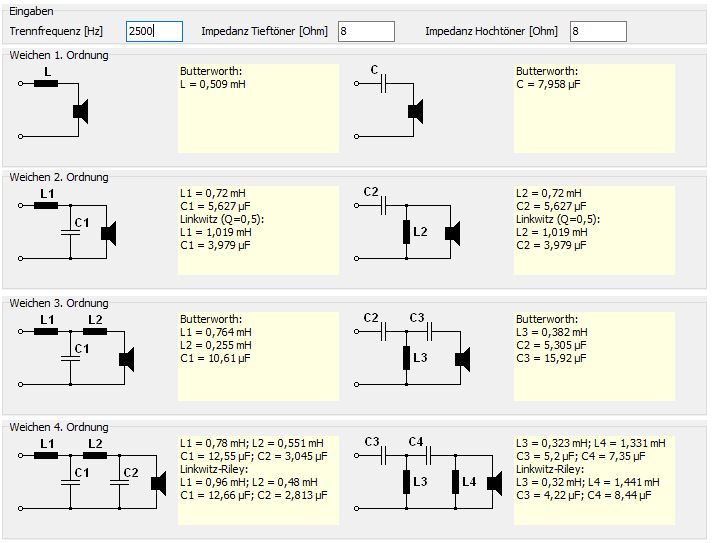Weichenrechner mit Ausgabe der Werte für eine Trennfrequenz von 2,5kHz
Der Rechner bietet die Möglichkeit, Weichen mit 4 unterschiedlichen Flankensteilheiten zu berechnen. In unserem Beispiel werden wir eine Weiche 2. Ordnung und eine mit 3. Ordnung aufbauen. Das sind die beiden in der Praxis am häufigsten vorkommenden Typen.
Zunächst simulieren wir die Weiche 2. Ordnung, die sogenannte 12dB Weiche nach der obigen Ausgabe
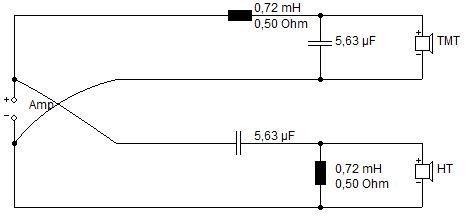Weiche 2. Ordnung (12dB)
Der resultierende Frequenzgang kommt einem Bergpanorama gleich
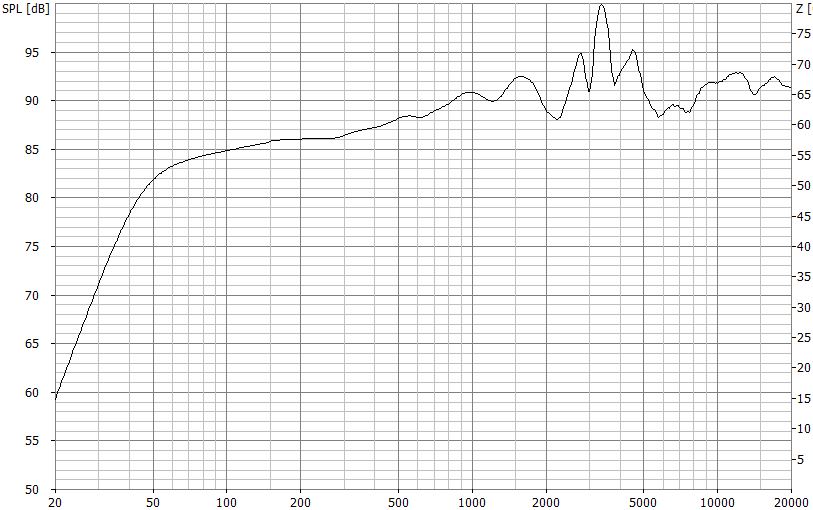Frequenzgang nach Beschaltung mit Weiche 2. Ordnung (12dB) aus dem Rechner
Der Frequenzgang steigt von den Bässen bis zu den Höhen um ca. 10dB an. Im Mitteltonbereich schlagen die heftigen Resonanzen des Tiefmitteltöners nahezu ungefiltert durch und überragen mit ihrer Spitze den ohnehin zu hohen Pegel nochmal um weitere 8dB. Der Lautsprecher wird bassarm sein und die durchschlagenden Resonanzen sorgen dafür, dass man sich von dem Lautsprecher angeschrien fühlt.
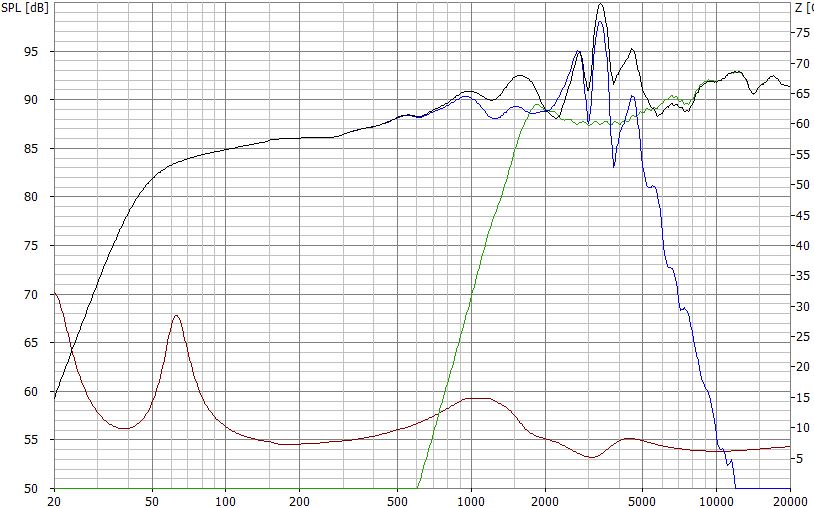
Frequenzgang mit Zweigen nach Beschaltung mit Weiche 2. Ordnung (12dB) aus dem Rechner
Die Zweige zeigen, dass die avisierte Übergangsfrequenz von 2,5 kHz nicht annähernd eingehalten wird. Der Hochtöner fällt erst unterhalb von etwa 1,5 kHz ab. Der Tief(mittel)töner reicht bis über 5 kHz, wobei seine Resonanzen quasi ungebremst ihr Unwesen treiben.
Simulieren wir halt einfach die Weiche 3. Ordnung (18dB) und schauen, ob die theroetisch steilere Trennung zu einem besseren Ergebnis führt.
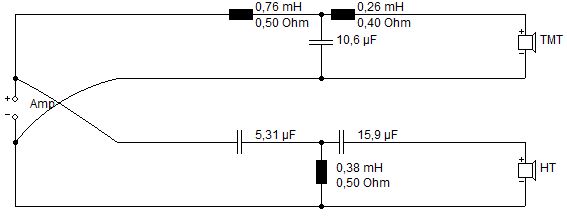Weiche 3. Ordnung (18dB)
Auch die steilere Beschaltung führt nicht zu einem wesentlich besseren Verhalten
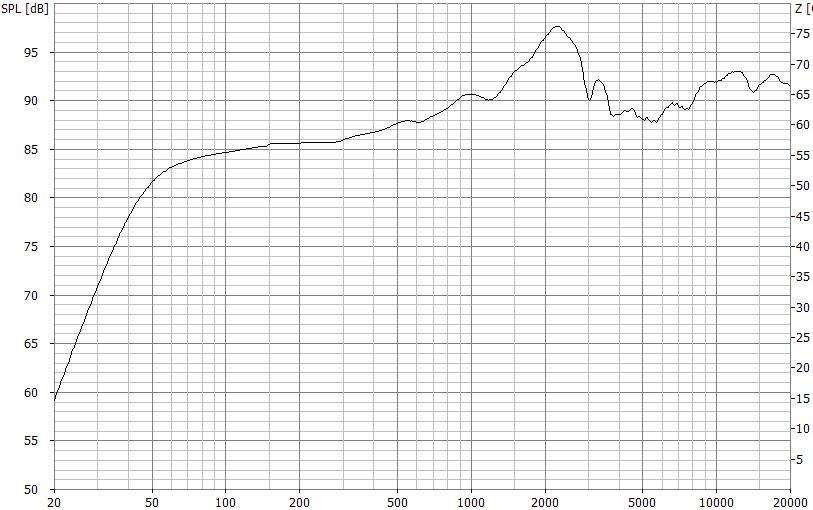
Frequenzgang nach Beschaltung mit Weiche 3. Ordnung (18dB) aus dem Rechner
Auch mit dieser Weiche schlagen die Resonanzen des Tief(mittel)töners durch, wenn auch nicht mehr ganz so stark wie bei der flacheren Weiche 2. Ordnung (12dB).
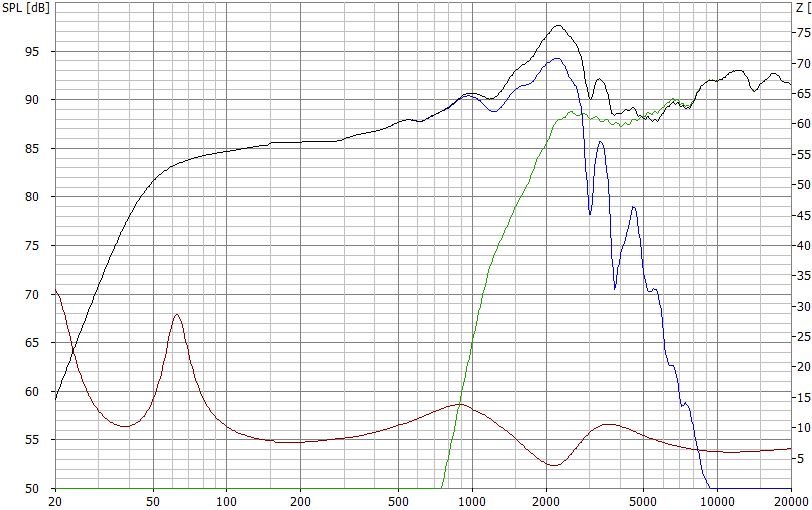
Frequenzgang mit Zweigen nach Beschaltung mit Weiche 3. Ordnung (18dB) aus dem Rechner
Auch hier zeigen die Einzelzweige die unzureichende Filterung, die diese einfache Weiche aus dem Rechner bewirkt.
Gleiches gilt übrigens auch für die vielerorts angebotenen Fertigweichen. Die darauf enthaltenen Filter sind, wenn überhaupt, ebenfalls nach dem gängigen Formelwerk dimensioniert.
Das nachfolgende Beispiel soll aufzeigen, wie der Lautsprecher mit einer durchentwickelten Frequenzweiche und einer sinnvoll gewählten Übergangsfrequenz funktionieren könnte, ohne jedoch in dieser Abhandlung näher auf die Entwicklung eingzugehen.
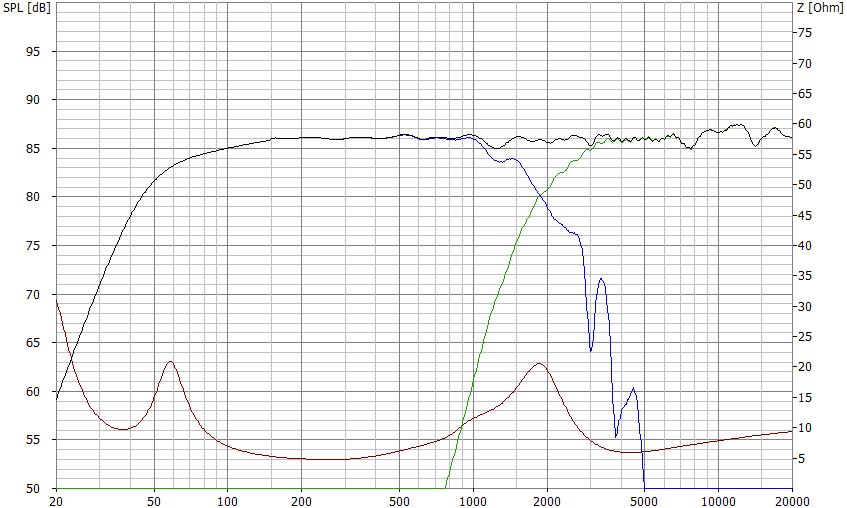Frequenzgang mit optimierter Weiche
Die zugehörige Weichenschaltung ist nicht mit einem Weichenrechner ermittelbar, aber grundsätzlich immer noch als relativ einfach zu bezeichnen.
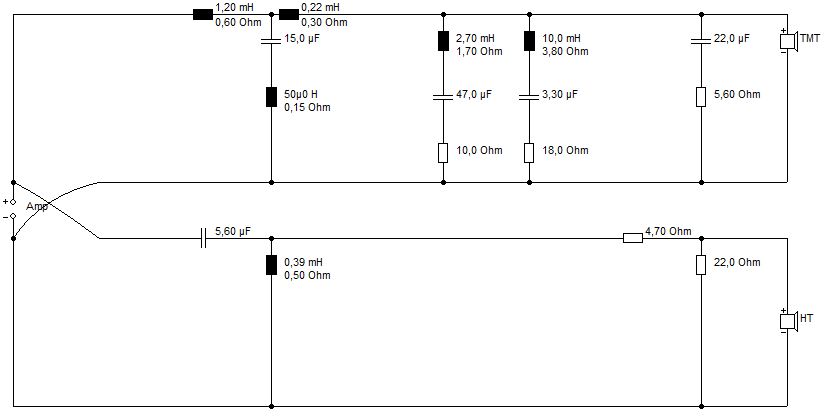Frequenzweiche optimiert
Wir haben nun gelernt, dass es unmöglich ist, einen gut funktionierenden Lautsprecher mit einer Frequenzweichenschaltung aus einem Rechner oder einer Fertigweiche aufzubauen. Diese Rechner arbeiten so lange genau, wie man sie für rein elektrische Schaltungen mit konstanten Lastwiderständen einsetzt. Da sie aber die akustischen Eigenschaften der einzelnen Chassis und die Einflüsse, die das Lautsprechergehäuse mitbringt, nicht berücksichtigen können, führen Berechnungen mittels solcher Rechner zu extremen Fehlfunktionen. Immer und ohne Ausnahme.
Wer wirklich daran interessiert ist, seine Lautsprecher selbst zu bauen, sollte entweder auf einen der vielen ausgereiften und durchentwickelten Bausätze zurückgreifen. Wenn der Lautsprecherbau aber zum Hobby werden soll, kommt der geneigte Interessent nicht umhin, sich in die Materie einzulesen und Messtechnik anzuschaffen.
36 Kommentare
Zum Kommentar-Formular springen
1. Also, habe ich die Sicherheit, dass die gekaufte Weichen (für die Bausätze) richtig gebaut sind ?
2. Ist es möglich eine Weiche mit 50 dB effektiv zu bauen ?
Danke für die Antwort
Autor
1. Das hängt davon ab, mit welcher Sorgfalt die Weichen zusammengebaut wurden. Das allein sagt aber über die Qualität eines Bausatzes nicht aus.
2. Das kann durchaus möglich sein. Aus eigener Erfahrung kann ich es aber nicht sagen.
Gruß
TYR
….endlich mal ein kleiner Beitrag,der den Blick weitet und der Akustik eine Chance gibt.
Vielen Dank für die mutigen Worte.
Gruß aus Kärnten
Autor
Herzlichen Dank…
Ohne dass der Beitrag meine eigentlichen Fragen beantwortet hat, sind jetzt alle Unklarheiten beantwortet und alle Fragen aus dem Weg geraeumt. Danke 🙂
Autor
Interessanter Kommentar. Danke…
Schöner Beitrag.
Half mir ebenfalls etwas Klarheit zu verschaffen.
Habe letztens einen Bluetooth Lautsprecher mit Dayton Chassis gebaut.
Die mit einem online Tool berechnete Weiche klingt echt mau.
Habe mich nun etwas mit VituixCAD beschäftigt, aber auch noch keine guten Ergebnisse erzielen können. Wie im Beispiel oben, habe ich diese Bergstruktur. Ich werde auch mal eine 18dB Weiche versuchen.
Danke für den Artikel, sehr interessant, die Gründe sind einleuchtend. Kann man an den Frequenzweichenbau methodisch herangehen, oder ist da eher Erfahrung und Intuition gefragt (ich vermute beides)? In welche Grundlagen müsste man sich einlesen, und welche Messtechnik müsste man dazu anschaffen?
Autor
Hallo Michael,
die Entwicklung einer Frequenzweiche gelingt natürlich besser, wenn eine gewisse Portion Erfahrung im Spiel ist. Intuition kommt dann wie von selbst ins Spiel. Messtechnik ist unabdingbar, um für Simulationen verwertbare Dateien zu generieren. Ich selbst verwende ein hochwertiges Messmikrofon welches trotz hoher Grundgenauigkeit zusätzlich noch über ein Korrekturfile verfügt, einen Mikrofonvorverstärker, eine umschaltbare Messbox, eine USB Soundkarte, sowie die Software ARTA. Es gibt alternative Software, wie z. B. REW. Da hat jeder seine eigenen Vorlieben.
Gutes Gelingen und viele Grüße,
Alex
Hallo Alex,
ein großartiger Beitrag ! Tausend Dank, für die viele Mühe.
Durch den Beitrag begebe ich mich gerade in eine gewisse Ernüchterung,
was die Berechnungen der idealen Frequenzweiche betrifft.
Ich versuche gerade einen E-Gitarren-Verstärker mit einem Hochtöner auszustatten, um
meine Akustik-Gitarre verwenden zu können.
Er normale Frequenzgang für E-Gitarren- Lautspreche geht meistens nicht über 5000Hz hinaus.
(Soll und muss er auch nicht)
Das Experiment funktioniert bereits schon einigermaßen brauchbar mit einem C von 1µF in Reihe
zu einem Piezzo-Hochtöner. Der Sound gefällt mir aber nicht besonders und ich werde es einmal mit einem
guten 8 Ohm Horn Hochtöner probieren.
Lieben Dank, noch mal für den tollen Beitrag !!!
Viele Grüße, Friedhelm
welchen Wert hat die mit 50mikr0H bezeichnete Spule im Tiefpass? o,5mH?
Wolfgang
Autor
Hallo Wolfgang,
der Spulenwert in dem Beispiel beträgt 50µH, also 0,05mH.
Gruß Alex
Hallo Alex
Würde sich denn ein iterativer Trial-and-Error Ansatz zur Frequenzweichen-Entwicklung anbieten? D.h. per Simulation mal eine initiale Schaltung erstellen (primär zur Festlegung der Trennfrequenzen) und dann in der Box messen. Anschliessend die lokalen „Unebenheiten“ mittels Korrekturen (veränderter Werte, Saugkreise hinzufügen, …) angehen und wieder messen. Oder wird man damit nur Bauteile und Kosten anhäufen ohne je auf ein gutes Resultat zu kommen?
Was hältst du eigentlich von DSP-Boards (https://auverdion.de/aurora-dsp/), die als programmierbaren Ersatz für die Frequenzweiche verwendet werden (d.h. jedes Chassis wird einzeln von einem Kanal des DSP angesteuert)?
Grüsse
André
Autor
Hallo André,
genau das ist es ja, was der Artikel beschreibt. Es ist notwendig, Messungen der unbeschalteten Chassis durchzuführen. Ob man sich dann eines Simulationstools bedient, oder ob man nach dem Try and Error Verfahren weiter arbeitet, spielt keine Rolle. Eine Simulation beschleunigt den Vorgang, da i. a. R. nicht oder nur im Detail nachgearbeitet werden muss. Natürlich kann man auch einen DSP einsetzen, wenn man das mag und Vorteile darin sieht. Das ist aber nicht Inhalt dieses Artikels.
Viele Grüße, Alex
Hallo Alexander ,
genauso ist es – die Berechnungen sind für “ feste “ werte. An Dynamik und Schwankungen im widerstand wird wohl nicht gedacht .Da taugen die Tabellen nicht. Das heißt ja auch Nennschein-widerstand. Hatte Anfang der Achtzigern ein Minibetrieb für PA und Musiker -Lautsprecher. Allein die Messgeräte hatten ein Vermögen verschlungen für Spektrum Messgeräte für Audio, Messmikrofon, RLC Messungen, hochwertiger Frequenzgenerator, temperierter Messraum,usw.,war noch nix mit PC.
Mit billig und ohne Erfahrung geht es meistens schief und es braucht Jahre und Geduld bis die Routine kommt.
Es ist ein Sog ;- ) immer noch…..
Autor
Hallo,
du sprichst mir aus der Seele. Manche wollen es aber immer noch nicht begreifen. Sie dengeln eine Kiste zusammen, schrauben x-beliebige Chassis und Weichen rein und freuen sich, dass Töne raus fallen. Klar, der „Entwickler“ Stolz ist in einem solchen ersten Moment ja auch toll, aber all diese Resultate sind weit entfernt von gutem Klang…
So long, Alex
Ein hoch interessanter Artikel über Lautsprecherweichen und deren Bemessung !
BRAVO dass jemand dazu endlich fachliches und fundiertes Wissen beiträgt !
Habe in den 70gern auch versucht Lautsprecher zu bauen – Katastrophe !!!
Dann habe ich mit 20 im Saturn-Köln mal im Studio 1 (Upperclass) mal zwischen den ganzen Transmissionline „Kühlschränken“ zwei winzige KEF 101 Referenz (1200 DM) gehöhrt. Wolte nicht glauben das es 2 kleine „Schuhkartongroße“ Kisten waren. Habe mich dann mal mit der Firma beschäftigt und die Broschüren KEF TOPICS reingezogen. Die hatten auch Bauvorschläge für Gehäuse und ihre Chassis (T10 und B110). Dann hatte ich es kapiert.
Eine Frequenzweiche muß individuell auf definierte Lautsprecher und exakt ein Gehäuse passen.
Abweichungen im Gehäuse won wenigen mm und Toleranzen der Lautsprecherpaare sowie Toleranzen der Frequenzweichenbauteile verderben alles.
TIP: Zieht euch mal die KEF-Topics und die Entwicklung der KEF Reference Lautsprecher rein.
Info: Bin inzwischen 70 und lausche immern noch gerne POP, Klassik und Jazz.
Nochmals Dank an den Autor dieser Seite für seine Aufklährungsarbeit.
Gruß Armin aus dem Rheinland
Autor
Hallo Armin,
vielen Dank für das Lob.
Viele Grüße, Alex
Nabend,
ich bin durch Zufall auf den Artikel aufmerksam geworden. Überall wird immer behauptet man müsse Berechnungen anstellen aber genau die hier gesammelten Erkenntnisse habe ich auch festgestellt.
Ich verfolge momentan einen anderen weg (2 Wege weiche). Ich habe Zugriff auf eine Aktiv Frequenzweiche (DCX2496) hier beschallte ich die Treiber über einen AMP direkt. Jetzt kann ich die Treiber ganz gezielt Trennen und bekomme so eine Vorstellung was die Berechnungen vorher gebracht haben (ohne unnötig Geld zu verbrennen für Bauteile oder Weichen)
Zu keinem Zeitpunkt hat die zuvor errechnete Weiche (XOver Punkt) gestimmt. Ich kann das momentan nur mit meinem Gehör gegenprüfen (suche noch nach passenden Messequipment).
Im letzten Beispiel sollte der TT bei 2khz getrennt werden 6db But und hat sich einfach katastrophal angehört.
Geworden ist es dann eine Weiche 3. Ordnung bei XOver 200hz (wirklich schlechter Treiber)
Ich Teste also erst und erstelle mir daraus dann eine Weiche, hat bisher gut geklappt im Gegensatz zu allen vorab Berechnungen.
Schöner Beitrag vielen Dank für die Erkenntnisse
Autor
Hallo Daniel,
toll, dass du den Artikel gefunden und auch gelesen hast. Natürlich kann man eine Weiche auch aktiv gestalten, was aber ohne Messequipment zu sehr ähnlichen Fehlern führt. Stellst du nämlich bei einer Aktivweiche oder einem DSP Übergangsfrequenzen ein, erfolgt die Trennung an konstanter Last vor den Endstufen elektrisch. Die Fehler, die durch den unsteten Impedanzverlauf der Chassis bei passiver Trennung auftreten, werden somit vermieden. Das ist es aber auch schon. Die Eigenheiten im Frequenzverlauf der Chassis, der Effekt des Baffle Step, Pegelunterschiede bei den Chassis und auch die Einflüsse, die das Gehäuse nimmt, bleiben unberücksichtigt. Als Beispiel habe ich eine kleine 2 Wege Box in der Simulation passiv mit einem 12dB Filter (2. Ordnung) mit Formelwerten für eine Trennung bei 2500 Hz beschaltet. Das Ergebnis ist dem in meinem Artikel nicht unähnlich.
Ersetzt man diese passive Weiche nun durch eine aktive mit identischer Trennfrequenz bei 2500Hz, stellt sich folgendes Verhalten ein:
Du siehst, dass das Resultat nicht sonderlich von der passiven Beschaltung, welche ich als Referenzprojekt hinterlegt habe, abweicht. Es sind also noch viele weitere Eckpunkte zu beachten, die ohne Messung auch bei aktiver Beschaltung nicht in den Griff zu bekommen sind. Deswegen ist auch die häufig zu findende Behauptung, aktiv sei alles viel einfacher und vor allem ohne Messungen abstimmbar, leider falsch. Wenn du dein Messequipment irgendwann einsatzfähig hast, wirst du dies problemlos nachvollziehen können.
Viel Spaß weiterhin und viele Grüße
Alex
Hallo Alex,
Danke für des aufschlussreichen Artikel.
Die Funktion deiner optimierten Frequenzweiche ist mir soweit klar. Nur habe ich mich gefragt welche Funktion die 50uH Spule, welche in Reihe zum Kondensator des Tiefpasses geschalten ist übernimmt.
LG Lukas
Autor
Hallo Lukas,
die dem Parallelkondensator nachgeschaltete 0,05mH Spule unterdrückt die Resonanzspitze in der zur Trennfrequenz hin abfallenden Flanke des Tiefmitteltöners um einige dB. So kann sich diese nicht mehr negativ auf den Frequenzgang und somit den Klang des Lautsprechers auswirken.
Viele Grüße, Alex
Hallo Alex,
ich bin eben zufällig auf Ihre Homepage gestoßen und habe eine Frage zu diesem Artikel.
Vorneweg: einfach mit der gewünschten Trennfrequenz ein paar Bauteile ausrechnen und eine Holzkiste zusammenspaxen wird nicht zu einer guten Box führen – da sind sich wohl alle einig. Dass es Fertigweichen überhaupt gibt, werde ich nie verstehen.
Zu meiner Frage:
Die Screenshots sind eindeutig aus Boxsim und Sie erwähnen sogar das Tool. Boxsim bietet durchaus die Möglichkeit, die Parameter der Chassis einzupflegen oder Chassisdaten von Visaton zu nutzen, und damit dann eine Weiche zu simulieren. Darüber hinaus kann man das Gehäuse auslegen und weitere Details eingeben, wie etwa die Schallwandposition der Treiber, Ort und Menge der Bedämpung etc.. Tauscht man die Chassisdaten, kommt ein komplett anderes Ergebnis raus. Es kann also vieles, worüber hier steht, dass es unmöglich ist – außer messen natürlich.
Ist Ihnen diese Möglichkeit nicht bekannt, oder für Sie nicht zufriedenstellend im Ergebnis?
Ich glaube nicht, dass Boxsim mit einem einfachen Widerstand als Last rechnet, sondern durchaus die Impedanzverläufe der Chassis berücksichtigt (Tool und Chassis sind in dem Fall beide von Visaton).
Aus eigener Erfahrung kann ich sagen, dass Boxsim durchaus eine brauchbare Basis für einen ordentlichen Lautsprecher liefern kann. Mit nachträglichen Korrekturen kann man auf jeden Fall Lautsprecher entwickeln, die von Fehlfunktionen weit entfernt sind und viel mehr für ein breites Grinsen im Gesicht des Entwicklers und seiner Besucher sorgen.
Tolle Seite hier, ich hätte auch gerne so viel Platz und Zeit für dieses Hobby.
Schöne Grüße
Autor
Hallo Willy,
Boxsim zählt zu den Simulationstools, und es arbeitet nicht mit dem bekannten Formelwerk, wie es die üblichen Frequenzweichen Berechnungstools machen. Ferner müssen in Boxsim die Amplitudenverläufe mit korrekter Phaseninformation, sowie die entsprechenden Impedanzverläufe der gemessenen Chassis eingepflegt werden. Wie sie selbst sagen, ist das Tool sogar in der Lage, das Verhalten im Tieftonbereich aus den TSP des TT bzw. TMT zu generieren. Wenn man die selbst angefertigten Messungen korrekt in Boxsim importiert, lässt sich damit durchaus ein Achsenfrequenzgang simulieren, der der Realität mindestens sehr nahe kommt und im besten Fall sogar deckungsgleich ist. Bis hierhin arbeitet das Programm zuverlässig. Leider ist das Tool nicht in der Lage, zusätzlich zum Achsenfrequenzgang weitere Winkelfrequenzgänge aus eigenen Messungen zu generieren. Diese werden in Boxsim nur auf Basis von Formelwerk errechnet. Mit der Realität hat das dann kaum mehr was zu tun. Die Abweichungen sind einfach zu groß, weil das Tool zu viele Faktoren, die eine reale Messung enthält, nicht exakt genug darstellen kann. Das reicht dann nur für eine überschlägige Darstellung. Selbst mit den in Boxsim hinterlegten Messungen der Visaton Chassis lassen sich keine wirklich zufriedenstellenden Lautsprecher aufbauen. Erst kürzlich habe ich einen Lautsprecher unter Verwendung zweier Visaton Chassis als Machbarkeitstudie in Boxsim simuliert. In der Realität waren stark abweichende Bauteilewerte nötig, um ein zufriedenstellendes Verhalten zu erzielen. Das liegt daran, dass der Algorithmus, mit dem die auf unendlicher Schallwand erfolgten Messungen von Boxsim auf das tatsächliche Gehäuse umgerechnet wird, zu viele Faktoren unberücksichtigt lässt, bzw, nicht nachstellen kann. In meinem Artikel geht es nur darum, aufzuzeigen, was bei bei einfacher Berechnung einer Weiche über das bekannte Formelwerk geschieht. Diese Formeln beziehen ja Frequenzgänge, Impedanzverläufe und die „Schweinereien“, die durch die Schallwandgeometrie entstehen, nicht ein. Auch in Bezug auf Letzteres zeigt der Artikel, was bei Veränderung einzelner Parameter geschieht.
Viele Grüße
Alex
Moin,
hervorragend und verständlich geschriebener Bericht.
Ich habe vor über 30 Jahren Boxen mit Fertigsätzen von Conrad gebaut. Die Lautsprechersätze waren von LAL, einst RFT aus der DDR.
Über die Jahre haben sich die Sicken der Tieftöner mehr oder weiniger aufgelöst, den Rest hat meine Tochter besorgt
Nach langer Suche habe ich Ersatz mit der Bauanleitung, die dem Bausatz seinerzeit beigelegt war, gefunden.
Hier ist auch der Schaltplan der Frequenzweiche abgebildet. Sämtliche Wert der Spulen und Kondensatoren weichen erheblich von den rechnerisch ermittelten Größen ab, was ich zunächst nicht verstanden habe. Dieser Bericht erklärt alles.
Danke dafür.
Grüße aus dem Rheingau
Autor
Hallo Robert,
danke für die Blumen.
VG, Alex
Hallo und guten Tag Alex
Ich befasse mich seit über 40 Jahren mit Hi Fi und High End , aber an die Entwicklung einer Weiche habe ich mich nie herangetraut. Ich weiß seit deinem Artikel jetzt auch warum. Du hast so viele fachliche gute Gründe geliefert die ich alle nachvollziehen kann und auch schon gehört oder gelesen habe. Allein die Fertigungstoleranzen der einzelnen Chassis oder die Toleranzen der Bauteile würden schon Romane füllen. Dank Deines Berichtes habe ich vieles verstanden und werde das Fach jetzt akribisch studieren und mir einige Messwerkzeuge zulegen (Aua das wird teuer wie zb. Oszilloskop, Sinus Generator etc.) Aber das geht step by step. Immer schön langsam. Ich hoffe noch mehr von Dir zu hören bzw zu lesen.
In diesem Sinne vielen Dank nochmals für die Inspiration eines schönes Hobbys weiterzuentwickeln.
Alles Gute
Andreas
Autor
Hallo Andreas,
vielen Dank für die Blumen. Schön, dass du dich einarbeiten und Messequipment anschaffen möchtest. Ein Oszilloskop und einen Sinusgenerator benötigst du aber eher nicht. Ein Soundkarten basiertes Messsystem wie ARTA oder REW ist eher zielführend.
Viele Grüße Alex
Guten Tag,
ich bin auf der Suche nach einem Programm um einen DSP fürs Auto mit frei einstellbaren Frequenzen und Flankensteilheiten besser einzustellen. Als Beispiel HT >1800 Hz mit 12dB, TMT muss dann bei Frequenz X und Filter Y laufen um bei der 1800Hz nicht zu überhöhen sondern wie bei Ihrem letzten Beispiel im Pegel linear zu laufen und ohne Überhöhung oder so?
Können Sie mir da weiter helfen?
Mit freundlichen Grüßen
Oliver Friedirch
Autor
Hallo Herr Friedrich,
mit DSP kenne ich mich nicht aus. Leider kann ich Ihre Frage deswegen nicht beantworten.
Viele Grüße
Alexander Gresler
Klingt halbwegs schlüssig und die ganzen 0815 Programme sind sowieso nix.
Vituixcad dagegen funktuoniert zu 100%! Vorausgesetzt man läd die richtige Messung ins Programm. Impedanzmessung im fertigen Gehäuse und auch ein Frequenzgangsmessung im fertigen Gehäuse. Die Simulation passt zu 95% zur praktischen Weiche! Und wer genau misst einen Frequenzgang in einer unendlichen Schallwand um eine Weiche zu entwickeln?
Als erstes berechnet man ein Gehäusevolumen und ein grobes Tuning falls es Bssreflex werden soll. Dann überlegt man wie die Box am ende ungefähr ausehen soll, dann baut man ein Testgehäuse und macht darin die Messungen.
Autor
Das klingt nicht nur halbwegs schlüssig, sondern vollkommen schlüssig. Ohne Messungen ist eine seröse Lautsprecherentwicklung nicht möglich. Das gilt sowohl für passive als auch aktive Konzepte. Und ja, die modernen Simulationsprogramme sind in der Lage Simulationen zu erstellen, die 100% mit der Realität übereinstimmen. Das beweist sich immer wieder aufs Neue. Das hängt lediglich von der Qualität der Messungen ab.
Guten Tag Herr Gresler,
danke für Ihr Feedback.
Meine Frage bezieht sich allgemein wie man den Punkt berechnet wenn die Frequenzweiche eingreift und wo der andere Lautsprecher dann mit der anderen Frequenz beschnitten werden muss damit in der Mitte beim Schnittpunkt kein Überhöhung auftritt. Wenn ich z.B. HT zu TMT bei 1600Hz trennen will und beide bei 1600Hz mit je 12dB Flanke würde ja eine leichte Überhöhung bei 1600Hz auftreten ?
Mfg
Oliver Friedrich
Autor
Hallo Herr Friedrich,
leider lässt sich das nicht errechnen. Es ist unumgänglich, die beteiligten Chassis im finalen Gehäuse, bzw. in einem Gehäuse, welches in Abmessungen und der Schallwandgeometrie dem finalen Gehäuse entspricht, zu messen. Diese Messungen können in ein Simulationsprogramm importiert werden, um eine entsprechende Schaltung zu simulieren. Mit modernen Simulationsmitteln und penibler Vorgehensweise gelingt das inzwischen so gut, dass man theoretisch am fertigen Objekt auf Kontrollmessungen verzichten könnte. Natürlich besteht auch die Möglichkeit auf eine Simulation zu verzichten und die passende Schaltung durch Wechsel von Bauteilen im Try & Error Verfahren zu ermitteln.
Viele Grüße
Alexander Gresler
Danke für das Feedback.
Dann werde ich am besten direkt im Auto den Frequenzgang messen und entsprechend einstellen.
Mit freundlichen Grüßen
Oliver F.
Autor
Dabei wünsche ich viel Erfolg.
Viele Grüße, Alex